Unsolvable Rubik's Cube Scrambles
When you take apart a Rubik's Cube and put it back together randomly, you have only a 1/12 chance of your scrambled configuration being solvable. In the case of other Rubik's Cube variations where the orientation of the center piece also counts the chances are even smaller.
If the online Rubik's solver throws the 'Invalid scramble' error, first you need to double-check your puzzle and make sure you have entered the color of each field correctly.
If you keep getting this error then you'll have to disassemble and rebuild your cube in the solved position because it has an unsolvable state.
Examples of Impossible Scrambles
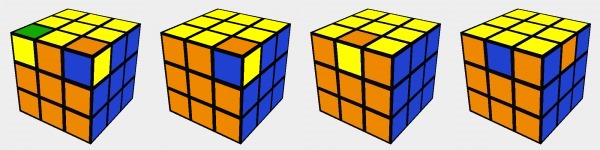
Not every random scramble can be solved by legal moves because of the parity which refers to whether a permutation is even or odd (can that permutation be represented by an even or odd number of swaps):
- Corner orientation
Each corner piece has three possible orientations. It can be oriented correctly (0), clockwise (1) or counterclockwise (2). The sum of corner orientations always remain divisible by 3, no matter how many legal turns you make. See the first two cases on the image. - Edge orientation
Each legal rotation on the Rubik's Cube always flips an even number of edges so there can't be only one piece oriented wrong. See the third example. - Piece swaps
Considering the permutation of all the corners and edges, the overall parity must be even which means that each legal move always performs the equivalent of an even number of swaps (ignoring orientation). See the last example.

Combining all these laws we get 1/3 * 1/2 * 1/2 = 1/12
Experienced cubers notice that something's wrong when they reach the last layer of the puzzle.
These scrambles can't be solved; you have to take your cube apart to fix it.
Unsolvable Cubes In Artworks
When artists, advertisers, or animators feature a Rubik's Cube in their work—whether it's in a cartoon, drawing, or advertisement—they often display only three visible faces. An experienced cuber can usually spot mistakes at a glance—sometimes to the point where it even hurts their eyes ʕ͡ಥω͡ಥʔ

A Rubik's Cube has a blue-blue edge in The Plucky Squire video game by Nintendo
Can you find other errors?
⚠️ If you're an artist, it's best to copy an actual physical cube rather than randomly placing the six colors on the empty cube.
Common mistakes that are easy to spot include:
- A color being used more than once as a center piece
- A corner or edge having the same color appear more than once.
- An edge piece showing colors from opposite sides (a yellow-white edge).
- The same edge piece appearing twice.
Understanding these limitations can shed light on how often media unintentionally features impossible cubes without realizing it.
An interesting mathematical question: What is the probability that a visible sticker arrangement on three faces allows for a solvable configuration on the unseen three faces? This becomes even more complex when considering two scenarios: one where the standard color scheme is enforced (with opposite colors like white–yellow, red–orange, and green–blue) and another where any color arrangement is allowed.
Impossible Stickering
While most unsolvable Rubik's Cubes result from incorrect reassembly, another cause is impossible stickering. This happens when the stickers are applied randomly to a scrambled cube, creating configurations that are impossible to solve.
A simple example: once you placed a white center sticker, you can't have another white center.
Random stickering probably violates one of these rules:
-
Color Distribution Issues: A standard cube has 6 colors with exactly 9 stickers each. Random stickering can result in color imbalances—like 10 red stickers and 8 blue—making it unsolvable.
-
Permutation Parity Violations: Even with correct colors, the arrangement might represent an impossible permutation. Legal moves allow only even permutations of corners and edges. Random stickering can create odd parity mismatches.
-
Orientation Constraints: The sum of all corner twists must be a multiple of 3, and flipped edges must be even. Random placement often violates these constraints.
What Are The Chances of Correctly Applying the Stickers?
The chance of ending up with a solvable cube after random stickering is incredibly small:
-
The cube has about 43 quintillion solvable positions. That falls between 20! and 21!
-
There are 54! (1*2*3*4*...*53*54) possible sticker arrangements.
We have to divide these two, which results in roughly 1 / (21*22*23*...*53*54) to get the probability of achieving a solvable configuration is 1 in 10^50 which is close to zero. So make sure to apply the stickers in a solved order, not just randomly.
Example of Bad Stickering

The image above shows another invalid cube but this case can't be reached by taking apart the puzzle and assembling it incorrectly. This has been stickered wrong and it has never been solvable. Let's see why!
According to the center pieces the white face has to be on the top, but there's an orange-blue-yellow corner that would put the yellow on the top when the orange is on the front and the blue on the right.
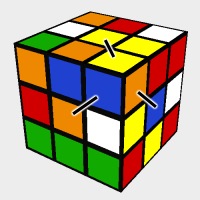
We can never have a white-yellow edge piece when the white and yellow center pieces are on the opposite sides of the cube.